Percent error

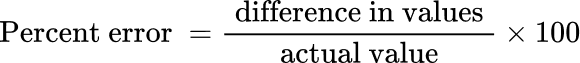
Here you will learn about percent error, including how to calculate it and use it to solve problems.

Students first learn about percent error in the 7 th grade and expand this knowledge as they move through middle school and high school statistics.

What is percent error?

Percent error is a type of percent problem that describes the difference between an estimated, observed, or experimental value, and an actual, accepted, or real value as a percent of the actual value. In other words, percent error is how big your error is when you estimate a measurement. In experimentation, it can tell you how far off your observed value is from the true, accepted value. This can help in evaluations and adjustments in various scientific and statistical applications including science, engineering, and finance.

The way you calculate a percent error is similar to how you calculate a percent change (percentage change).

To calculate the percent error you can apply the following formula:

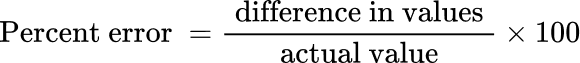
In chemistry, physics and other sciences, the actual value or theoretical value can be the established value you would expect as a result of an experiment. For example, the actual value of the boiling point of water is 100℃ .

The actual value is important for the following three reasons:

1. Baseline for comparison: Theoretical values act as a standard or expected result that experimental values are compared against.
2. Accuracy check: By comparing an experimental result to the theoretical value, scientists can calculate the percent error. This calculation highlights the accuracy and precision of the experiment.
3. Error measurement: Theoretical value is used at the base of the percent error formula (in the denominator), crucial for quantifying the deviation of the experimental result from the expected one.

The difference in values is the positive difference between the estimated value and the actual value (or the absolute value of the error). This is also known as the absolute error.

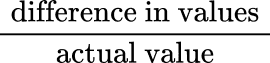
The ratio of the difference in values to the actual value, , is known as the relative error.

Let’s look at an example where percent error can be applied in real-life scenarios.

Lucas estimated the weight of his pet rabbit, Blu, to be 5.5 pounds. Blu’s actual weight is 4.75 pounds. Find the percent error.

Using the formula,

Lucas’s percent error is 15.8 \% meaning his estimate was about 15.8 \% off from the actual weight measurement.